There are n computers numbered from 0 to n - 1 connected by ethernet cables connections forming a network where connections[i] = [ai, bi] represents a connection between computers ai and bi. Any computer can reach any other computer directly or indirectly through the network.

You are given an initial computer network connections. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected.

Return the minimum number of times you need to do this in order to make all the computers connected. If it is not possible, return -1.

Example

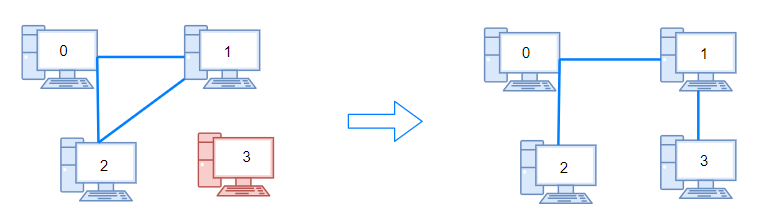
Input: n = 4, connections = [[0,1],[0,2],[1,2]]
Output: 1
Explanation: Remove cable between computer 1 and 2 and place between computers 1 and 3.

Solution

/**
 * @param {number} n
 * @param {number[][]} connections
 * @return {number}
 */
var makeConnected = function (n, connections) {
  //if the number of connections is less than n-1, return -1
  if (connections.length < n - 1) return -1;
  //create a graph
  const graph = new Array(n).fill().map(() => []);
  //create a set to keep track of visited nodes
  const visited = new Set([]);
  //add the connections to the graph
  for (const [v1, v2] of connections) {
    //add the connection to the graph
    graph[v1].push(v2);
    //add the connection to the graph
    graph[v2].push(v1);
  }
  //start at node 0
  const queue = [0];
  //add node 0 to the visited set
  visited.add(0);
  let ans = 0;
  //while the queue is not empty
  while (queue.length > 0) {
    //get the current node
    const node = queue.shift();
    //loop through the neighbors
    for (const neighbor of graph[node]) {
      //if the neighbor is not visited
      if (!visited.has(neighbor)) {
        //add the neighbor to the visited set
        visited.add(neighbor);
        //add the neighbor to the queue
        queue.push(neighbor);
      }
    }
    //if the queue is empty
    if (queue.length === 0) {
      //loop through the graph
      for (let i = 0; i < graph.length; i++) {
        //if the node is not visited
        if (!visited.has(i)) {
          //add the node to the visited set
          visited.add(i);
          //add the node to the queue
          queue.push(i);
          //increment the answer
          ans++;
          //break out of the loop
          break;
        }
      }
    }
  }
  return ans;
};