You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

Return the number of pairs of different nodes that are unreachable from each other.

Example

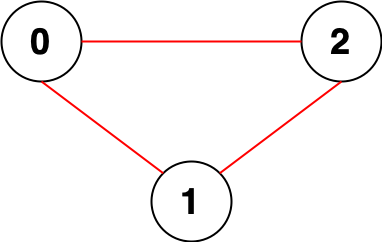
Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

Solution

This one was extremely tough, I found a solution here

var countPairs = function (n, edges) {
  // create an adjacency list
  const adj = [];

  for (let i = 0; i < n; i++) {
    // create an array for each node
    adj.push([]);
  }

  for (let [from, to] of edges) {
    // add the edges to the adjacency list
    adj[from].push(to);
    adj[to].push(from);
  }

  // create a set to keep track of visited nodes
  const visited = new Set();

  function dfs(from) {
    visited.add(from);

    let count = 1;

    for (const to of adj[from]) {
      // if the node has not been visited, add it to the count
      if (!visited.has(to)) {
        count += dfs(to);
      }
    }

    return count;
  }

  const groups = [];

  for (let i = 0; i < n; i++) {
    if (!visited.has(i)) {
      const count = dfs(i);
      groups.push(count);
    }
  }

  let ans = 0;

  for (let i = 0; i < groups.length - 1; i++) {
    for (let j = i + 1; j < groups.length; j++) {
      ans += groups[i] * groups[j];
    }
  }
  return ans;
};