You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.

The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.

Return the length of the longest cycle in the graph. If no cycle exists, return -1.

A cycle is a path that starts and ends at the same node.

Example

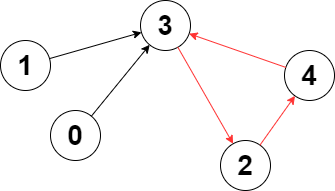
Input: edges = [3,3,4,2,3]
Output: 3
Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2.
The length of this cycle is 3, so 3 is returned.

Solution

Good solution found here

const longestCycle = (edges) => {
  let n = edges.length,
    g = Array(n).fill(-1);
  for (let i = 0; i < n; i++) {
    if (edges[i] != -1) g[i] = edges[i];
  }
  return detectLongestCycleDG(g);
};

// direct parent -> child, no queue
const detectLongestCycleDG = (g) => {
  // each node's child <= 1
  let n = g.length,
    cycleStart = Array(n).fill(-1),
    dis = Array(n).fill(Number.MAX_SAFE_INTEGER),
    res = -1;
  for (let i = 0; i < n; i++) {
    if (cycleStart[i] == -1) {
      // current node should not under any other cycle, can be as a cycle start node
      let cur = i,
        step = 0;
      while (1) {
        if (dis[cur] != Number.MAX_SAFE_INTEGER) {
          if (cycleStart[cur] == i) {
            // cycle find
            res = Math.max(res, step - dis[cur]);
          }
          break;
        }
        dis[cur] = step;
        cycleStart[cur] = i; // set cycle start node to current node
        cur = g[cur];
        step++;
      }
    }
  }
  return res;
};