There are n piles of coins on a table. Each pile consists of a positive number of coins of assorted denominations.

In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.

Given a list piles, where piles[i] is a list of integers denoting the composition of the ith pile from top to bottom, and a positive integer k, return the maximum total value of coins you can have in your wallet if you choose exactly k coins optimally.

Example

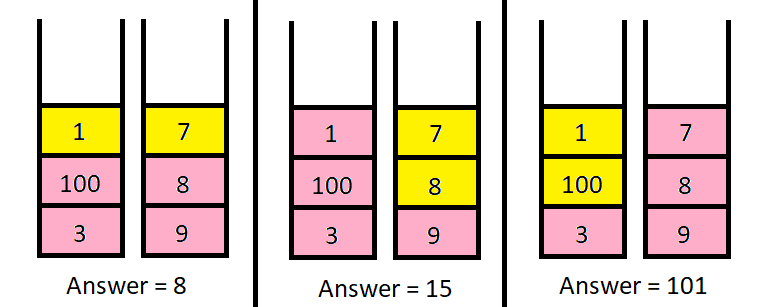
Input: piles = [[1,100,3],[7,8,9]], k = 2
Output: 101
Explanation:
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.

Solution

Great solution found here.

/**
 * @param {number[][]} piles
 * @param {number} k
 * @return {number}
 */
var maxValueOfCoins = function (piles, k) {
  // array of length k pre-filled with zeros
  // each value dp[i] will denote the max value we can get with i-1 coins
  let dp = Array(k).fill(0);

  // for each pile
  for (const pile of piles) {
    const tmp = Array(k).fill(0);

    let sum = 0;
    for (let i = 0; i < k && i < pile.length; i++) {
      // presum coin values for each pile
      sum += pile[i];

      for (let j = i; j < k; j++) {
        // for each value in dp array
        // check what max value we can get
        // if we'll get i coins from the current pile
        // and all the rest coins from the previous piles
        tmp[j] = Math.max(
          tmp[j],
          dp[j],
          sum + (j - i - 1 >= 0 ? dp[j - i - 1] : 0)
        );
      }
    }
    dp = tmp;
  }

  return dp[k - 1];
};