Given the root of a binary tree, return the maximum width of the given tree.

The maximum width of a tree is the maximum width among all levels.

The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.

It is guaranteed that the answer will in the range of a 32-bit signed integer.

Example

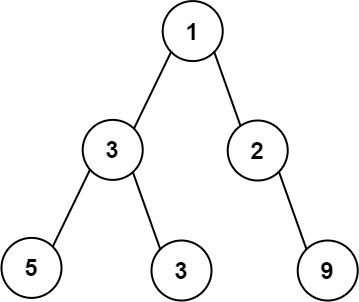
Input: root = [1,3,2,5,3,null,9]
Output: 4
Explanation: The maximum width exists in the third level with length 4 (5,3,null,9).

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var widthOfBinaryTree = function (root) {
  //Set minPos and maxWidth to 0
  const minPos = [0];
  let maxWidth = 0;

  //Call DFS function, then return result
  callDFS(root, 0, 0);
  return maxWidth;

  function callDFS(node, level, pos) {
    //If node is null, return
    if (!node) return;
    //If minPos at level is undefined, set it to pos
    if (minPos[level] === undefined) minPos.push(pos);

    //Calculate diff between pos and minPos at level
    const diff = pos - minPos[level];
    //Set maxWidth to max of maxWidth and diff+1
    maxWidth = Math.max(maxWidth, diff + 1);

    //Call DFS on left and right nodes
    callDFS(node.left, level + 1, diff * 2);
    //
    callDFS(node.right, level + 1, diff * 2 + 1);
  }
};