Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi] represents a directed edge from node fromi to node toi.

Find the smallest set of vertices from which all nodes in the graph are reachable. It’s guaranteed that a unique solution exists.

Notice that you can return the vertices in any order.

Example

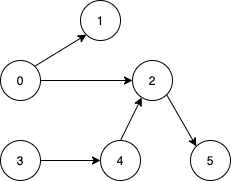
Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
Output: [0,3]
Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].

Solution

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number[]}
 */
var findSmallestSetOfVertices = function (n, edges) {
  //Declare result array and set
  let result = [];
  let set = new Set();
  //FOR the length of edges
  for (let i = 0; i < edges.length; i++) {
    //Add the second value of each edge to the set
    set.add(edges[i][1]);
  }
  //FOR the length of n
  for (let i = 0; i < n; i++) {
    //IF the set does not have i
    if (!set.has(i)) {
      //Push i to the result array
      result.push(i);
    }
  }
  return result;
};