Given a wooden stick of length n units. The stick is labelled from 0 to n. For example, a stick of length 6 is labelled as follows:

Given an integer array cuts where cuts[i] denotes a position you should perform a cut at.

You should perform the cuts in order, you can change the order of the cuts as you wish.

The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.

Return the minimum total cost of the cuts.

Example

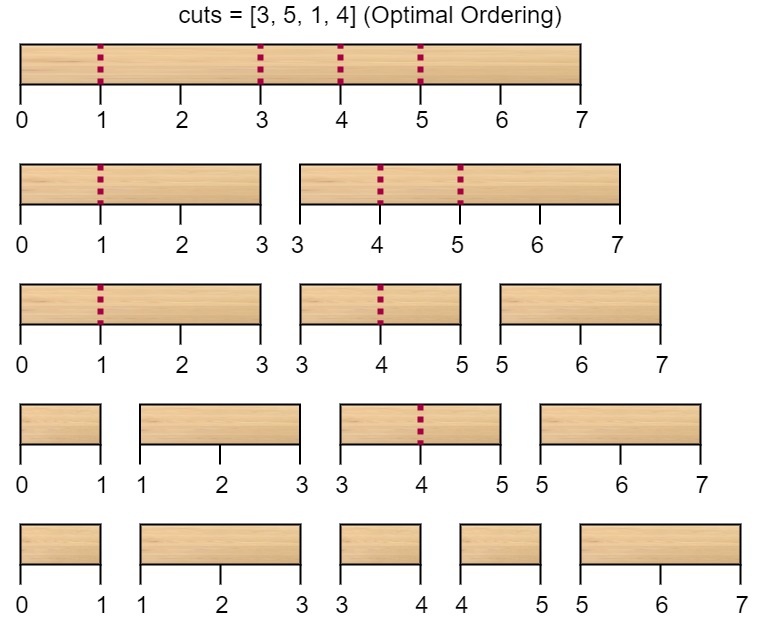
Input: n = 7, cuts = [1,3,4,5]
Output: 16
Explanation: Using cuts order = [1, 3, 4, 5] as in the input leads to the following scenario:

Solution

Great solution found here

/**
 * @param {number} n
 * @param {number[]} cuts
 * @return {number}
 */
var minCost = function (n, cuts) {
  //Sort the cuts
  cuts.sort((a, b) => a - b);
  //Add 0 and n to the cuts array
  cuts = [0, ...cuts, n];
  //Declare the length of the cuts array
  const stickLen = cuts.length;
  //Declare the dp array
  const dp = Array(stickLen)
    .fill(0)
    //Map over the dp array
    .map(() => Array(stickLen).fill(0));

  //recursive for loop to find the minimum cost
  for (let i = stickLen - 2; i >= 0; i--) {
    for (let j = i + 2; j < stickLen; j++) {
      let minCost = Infinity;
      for (let k = i + 1; k < j; k++) {
        //Find the minimum cost
        const cost = cuts[j] - cuts[i] + dp[i][k] + dp[k][j];
        //Set the minimum cost
        minCost = Math.min(minCost, cost);
      }
      //Set the dp array
      dp[i][j] = minCost;
    }
  }
  return dp[0][stickLen - 1];
};