Given an array nums that represents a permutation of integers from 1 to n. We are going to construct a binary search tree (BST) by inserting the elements of nums in order into an initially empty BST. Find the number of different ways to reorder nums so that the constructed BST is identical to that formed from the original array nums.

For example, given nums = [2,1,3], we will have 2 as the root, 1 as a left child, and 3 as a right child. The array [2,3,1] also yields the same BST but [3,2,1] yields a different BST. Return the number of ways to reorder nums such that the BST formed is identical to the original BST formed from nums.

Since the answer may be very large, return it modulo 109 + 7.

Example

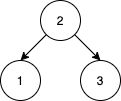
Input: nums = [2,1,3]
Output: 1
Explanation: We can reorder nums to be [2,3,1] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.

Solution

Great solution found here

// Main Function
var numOfWays = function (nums) {
  return (helper(nums) - 1n) % BigInt(1e9 + 7); // Return modulo value
};

// Function return combination (Mathematics) [Formula = n!/( k!*(n-k)!)]
var nCr = (n, r) => {
  if (n < 2) return 1n;
  (n = BigInt(n)), (r = BigInt(r));
  return fact(n) / (fact(n - r) * fact(r));
};

const cache = new Map(); // Chache for factorials
// Returns factorial of n [Formula = n!]
var fact = (n) => {
  if (n < 2) return 1n;
  if (cache.has(n)) return cache.get(n);
  const res = BigInt(n) * fact(n - 1n);
  cache.set(n, res);
  return res;
};

var helper = (nums) => {
  if (nums.length < 3) return 1n;

  const left = [],
    right = [];
  // Separate lower and higher values than first element in nums
  for (let i = 1; i < nums.length; ++i) {
    if (nums[i] < nums[0]) left.push(nums[i]);
    if (nums[i] > nums[0]) right.push(nums[i]);
  }

  // Number of possible combinations to get left and right separated
  const comb = nCr(nums.length - 1, left.length);
  return comb * helper(left) * helper(right);
};